周志华《机器学习》习题解答：Ch4.4 - 编程实现CART算法与剪枝

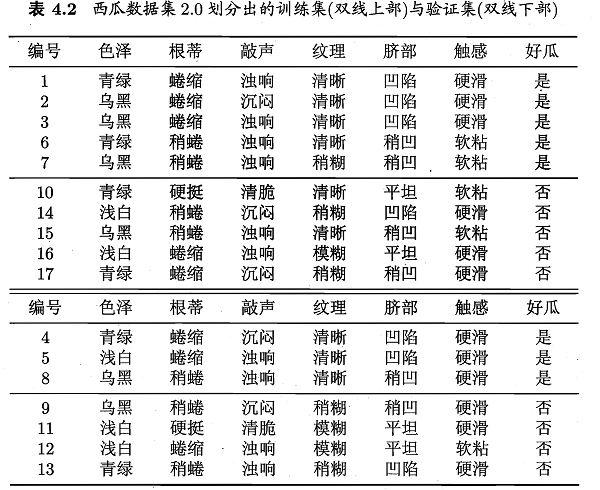
基于训练集构建的完全决策树易陷入过拟合，为提升模型泛化能力，通常需要对树进行剪枝。此处基于基尼系数构建出决策树（CART算法），然后编程实现预剪枝和后剪枝操作，最后分析了他们的作用。

本文编程采用Python实现，相关源码托管于Github：PnYuan/Machine-Learning_ZhouZhihua，欢迎访问。

问题回顾

• 决策树基于训练集完全构建易陷入过拟合。为提升泛化能力。通常需要对决策树进行剪枝。

• 原始的CART算法采用基尼指数作为最优属性划分选择标准。

编码基于Python实现，详细解答和编码过程如下：（查看完整代码和数据集）：

解题过程

最优划分属性选择 - 基尼指数

同信息熵类似，基尼指数（Gini index）也常用以度量数据纯度，一般基尼值越小，数据纯度越高，相关内容可参考书p79，最典型的相关决策树生成算法是CART算法。

下面是某属性下数据的基尼指数计算代码样例（连续和离散的不同操作）：

def GiniIndex(df, attr_id):
    '''
    calculating the gini index of an attribution
     
    @param df:      dataframe, the pandas dataframe of the data_set
    @param attr_id: the target attribution in df
    @return gini_index: the gini index of current attribution
    @return div_value: for discrete variable, value = 0
                   for continuous variable, value = t (the division value)
    '''  
    gini_index = 0  # info_gain for the whole label
    div_value = 0  # div_value for continuous attribute
    
    n = len(df[attr_id])  # the number of sample
    
    # 1.for continuous variable using method of bisection
    if df[attr_id].dtype == (float, int):
        sub_gini = {}  # store the div_value (div) and it's subset gini value
        
        df = df.sort([attr_id], ascending=1)  # sorting via column
        df = df.reset_index(drop=True)
        
        data_arr = df[attr_id]
        label_arr = df[df.columns[-1]]
        
        for i in range(n-1):
            div = (data_arr[i] + data_arr[i+1]) / 2
            sub_gini[div] = ( (i+1) * Gini(label_arr[0:i+1]) / n ) \
                              + ( (n-i-1) * Gini(label_arr[i+1:-1]) / n )
        # our goal is to get the min subset entropy sum and it's divide value
        div_value, gini_index = min(sub_gini.items(), key=lambda x: x[1])
        
    # 2.for discrete variable (categoric variable)
    else:
        data_arr = df[attr_id]
        label_arr = df[df.columns[-1]]
        value_count = ValueCount(data_arr)
            
        for key in value_count:
            key_label_arr = label_arr[data_arr == key]
            gini_index += value_count[key] * Gini(key_label_arr) / n
    
    return gini_index, div_value

---

完全决策树生成

下图是基于基尼指数进行最优划分属性选择，然后在数据集watermelon-2.0全集上递归生成的完全决策树。(基础算法和流程可参考题4.3，或查看完整代码）

---

剪枝操作

参考书4.3节（p79-83），剪枝是提高决策树模型泛化能力的重要手段，一般将剪枝操作分为预剪枝、后剪枝两种方式，简要说明如下：

剪枝类型	搜索方向	方法开销	结果树的大小	拟合风险	泛化能力
预剪枝（prepruning）	自顶向下	小（与建树同时进行）	很小	存在欠拟合风险	较强
后剪枝（postpruning）	自底向上	较大（决策树已建好）	较小		很强

基于训练集与测试集的划分，编程实现预剪枝与后剪枝操作：

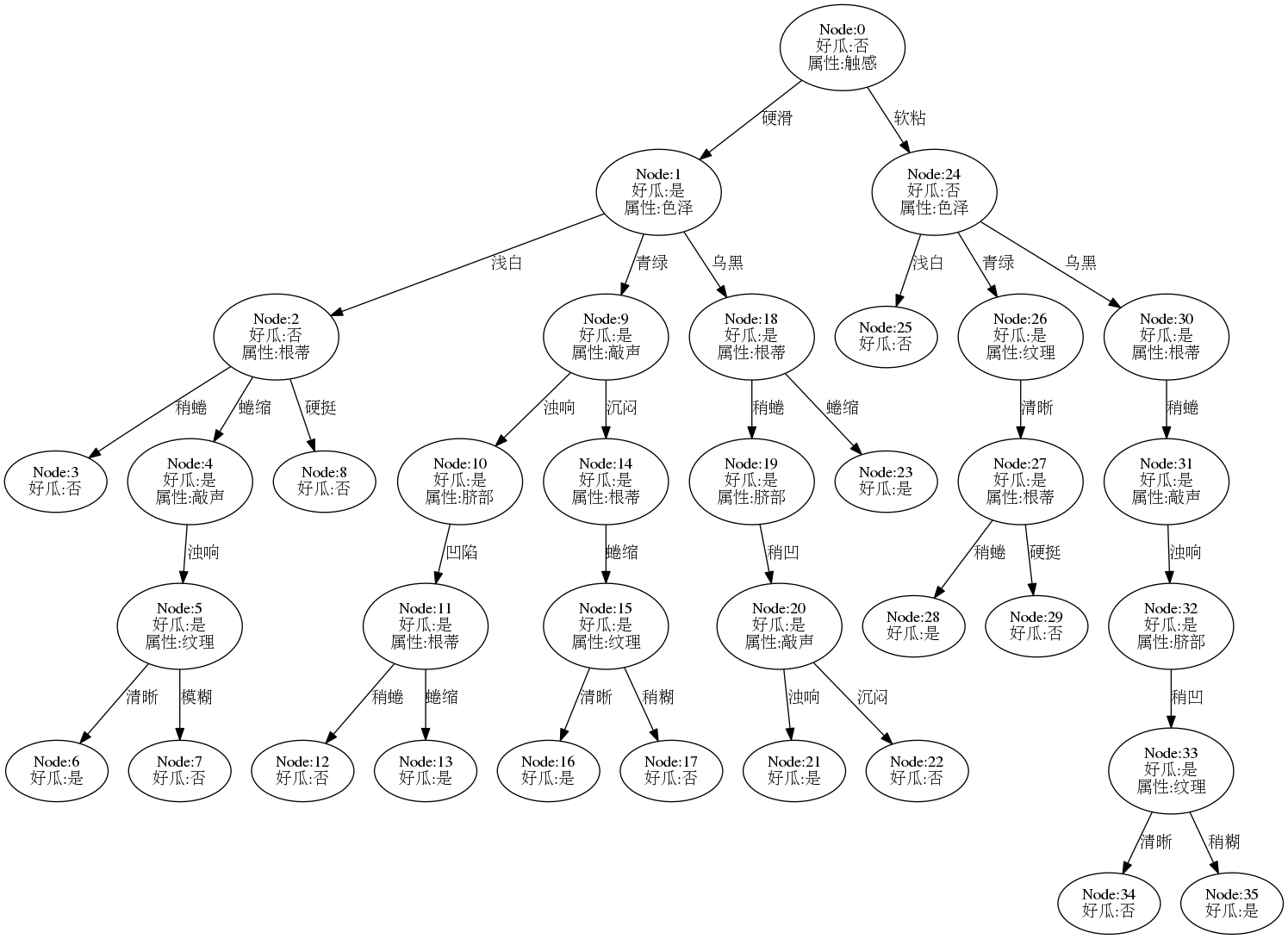
完全决策树

下图是基于训练集生成的完全决策树模型，可以看到，在有限的数据集下，树的结构过于复杂，模型的泛化能力应该很差：

此时在测试集（验证集）上进行预测，精度结果如下：

accuracy of full tree: 0.571

预剪枝

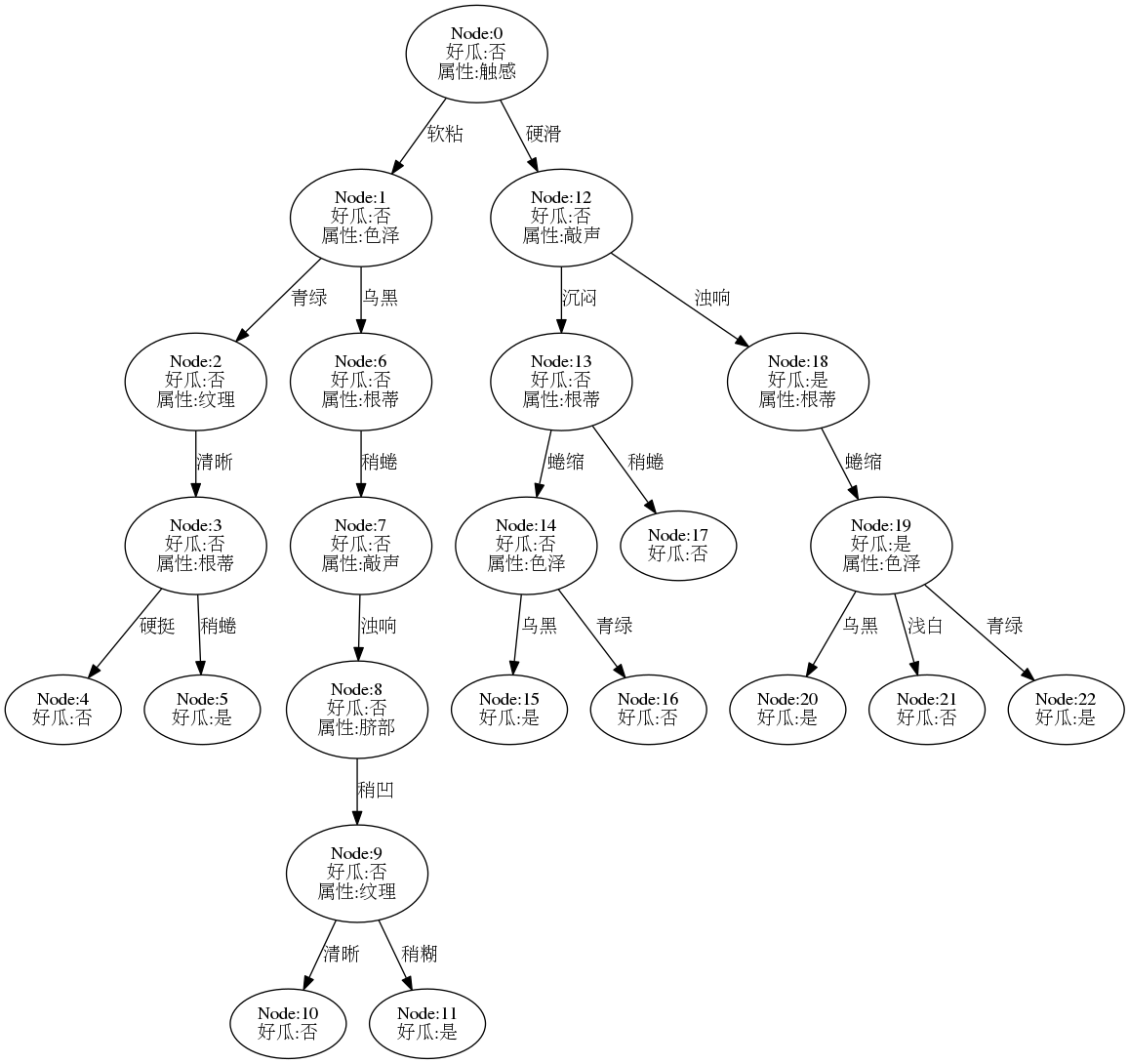
参考书p81，采用预剪枝生成决策树，查看相关代码， 结果树如下：

现在的决策树退化成了单个节点，（比决策树桩还要简单），其测试精度为：

accuracy of pre-pruning tree: 0.571

此精度与完全决策树相同。进一步分析如下：

• 基于奥卡姆剃刀准则，这棵决策树模型要优于前者；
• 由于数据集小，所以预剪枝优越性不明显，实际预剪枝操作是有较好的模型提升效果的。
• 此处结果模型太简单，有严重的欠拟合风险。

后剪枝

参考书p83-84 ，采用后剪枝生成决策树，查看相关代码，结果树如下：

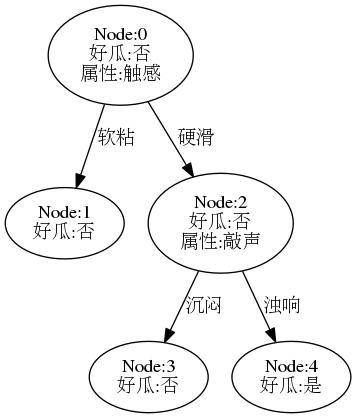
决策树相较完全决策树有了很大的简化，其测试精度为：

accuracy of post-pruning tree: 0.714

此精度相较于前者有了很大的提升，说明经过后剪枝，模型泛化能力变强，同时保留了一定树规模，拟合较好。

本题小结

• 由于本题数据集较差，决策树的总体表现一般，交叉验证存在很大波动性。
• 剪枝操作是提升模型泛化能力的重要途径，在不考虑建模开销的情况下，后剪枝一般会优于预剪枝。
• 除剪枝外，常采用最大叶深度约束等方法来保持决策树泛化能力。

---